7414. A simple task
You are given a
string S of length n and q queries. Each query has the
format i j k, meaning that you
need to sort the substring consisting of the characters from position I to j inclusive in non-decreasing order if k = 1, or
in non-increasing order if k = 0.
After processing
all the queries, print the resulting string.
Input. The first line contains two integers n and q (1 ≤ n ≤ 105, 0 ≤ q ≤ 50000) – the length of the
string and the number of queries, respectively.
The second line contains the string S, which consists only of lowercase
English letters.
Each of the next q lines contains three integers i, j and k (1 ≤ i
≤ j ≤ n, k
= 0 or k = 1) describing a
query.
Output. Print the string S after performing
all the queries.
|
Sample
input |
Sample
output |
|
10 5 abacdabcda 7 10 0 5 8 1 1 4 0 3 6 0 7 10 1 |
cbcaaaabdd |
SOLUTION
segment
tree
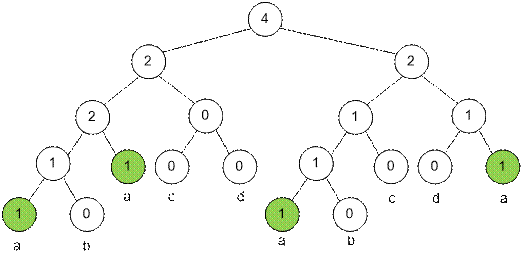
Let’s create 26 segment
trees for sums computation – one for each letter from ‘a’ to ‘z’.
Each tree must support multiple updates.
For example, for the
letter ‘a’ and the string “abacdabcda”, the corresponding segment
tree would look like this:
Using such a tree, we can
determine in logarithmic time how many times a given letter occurs in the range
[l; r].
Processing a query on the
range [l; r] reduces to counting sort. First, in the array cnt, we
count how many times each letter occurs within this range.
Then, depending on the
value of k, we “reconstruct” this section of the string:
·
if k = 1, the characters are arranged in non-decreasing order – that
is, from ‘a’ to ‘z’;
·
if k = 0, they are arranged in non-increasing order – from ‘z’ to ‘a’.
To do this, for the entire
range [l; r], for each letter ‘a’ + j, whose count is known
from the cnt array, we set the corresponding number of ones in the
segment tree, starting from position l (if sorting in ascending order)
or from position r (if sorting in descending order).
For example, suppose the
substring “acbdbcab” occupies positions [10; 17]. Let’s count the number
of occurrences of each letter in this range:
·
The letter ‘a’ occurs 2 times;
·
The letter ‘b’ occurs 3 times;
·
The letter ‘c’ occurs 2 times;
·
The letter ‘d’ occurs 1 time;
To sort the letters in the
range in ascending order, we first need to reset the values to 0 in the segment
tree of each letter over the interval [10; 17], and then perform the following
operations:
·
For the letter ‘a’ set each element in the
range [10; 11] to 1;
·
For the letter ‘b’ set each element in the range [12; 14] to 1;
·
For the letter ‘c’ set each element in the range [15; 16] to 1;
·
For the letter ‘d’ set each element in the range [17; 17] to 1;
Such “updates” to the
segment trees effectively simulate the permutation of characters over the
desired range without directly modifying the string itself.
After processing all
queries, the final string is reconstructed from the contents of the 26 segment
trees: for each letter, its tree is traversed sequentially, and at positions
where the value equals 1, the corresponding character is written into the resulting
string.
Algorithm implementation
For each letter from ‘a’ to ‘z’, we create a separate
segment tree. Thus, there are ALPHABET = 26 trees in total, each supporting sum
queries and multiple updates.
#define MAX 100010
#define ALPHABET 26
struct node
{
int sum, add;
}
SegTree[4*MAX][ALPHABET];
Declare an array to count the number of occurrences of each letter.
int cnt[ALPHABET];
Build 26 segment trees based on the string s – one for each letter
of the Latin alphabet.
void build(int v, int lpos, int rpos)
{
if (lpos == rpos)
{
SegTree[v][s[lpos] - 'a'].sum = 1;
for (int i = 0; i < ALPHABET; i++)
SegTree[v][i].add = -1;
}
else
{
int mid = (lpos + rpos) / 2;
build(v * 2, lpos, mid);
build(v * 2 + 1, mid + 1, rpos);
for (int i = 0; i < ALPHABET; i++)
{
SegTree[v][i].sum =
SegTree[v * 2][i].sum + SegTree[v * 2 + 1][i].sum;
SegTree[v][i].add = -1;
}
}
}
The vertex v corresponds to the segment [lpos, rpos], with mid = (lpos + rpos) / 2. Perform a push operation
for this vertex in the segment tree with index ver.
void Push(int v, int lpos, int mid, int rpos, int ver)
{
if (SegTree[v][ver].add != -1)
{
SegTree[2 * v][ver].add = SegTree[v][ver].add;
SegTree[2 * v][ver].sum = (mid - lpos + 1) * SegTree[v][ver].add;
SegTree[2 * v + 1][ver].add = SegTree[v][ver].add;
SegTree[2 * v + 1][ver].sum = (rpos - mid) * SegTree[v][ver].add;
SegTree[v][ver].add = -1;
}
}
The vertex v corresponds to the segment [lpos, rpos]. In the
segment tree with index ver, set the
value val for all elements with indices from left to right.
void SetValue(int v, int lpos, int rpos, int left, int right,
int val, int ver)
{
if (left > right) return;
if ((lpos == left) && (rpos == right))
{
SegTree[v][ver].add = val;
SegTree[v][ver].sum = (right - left + 1) * val;
return;
}
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos, ver);
SetValue(2 * v, lpos, mid, left, min(mid, right), val, ver);
SetValue(2 * v + 1, mid + 1, rpos, max(left, mid + 1), right,
val, ver);
SegTree[v][ver].sum =
SegTree[2 * v][ver].sum + SegTree[2 * v + 1][ver].sum;
}
The vertex v corresponds to the segment [lpos, rpos]. Find the sum of elements in the
range [left; right] in the segment tree with index ver.
int Summa(int v, int lpos, int rpos, int left, int right, int ver)
{
if (left > right) return 0;
if ((lpos == left) && (rpos == right)) return SegTree[v][ver].sum;
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos, ver);
return Summa(2 * v, lpos, mid, left, min(mid, right), ver) +
Summa(2 * v + 1, mid + 1, rpos, max(left, mid + 1), right, ver);
}
Perform a push operation on all vertices of the segment tree with index ver.
Then, insert the letter ver + ‘a’ into all positions of the
string s where its value in the segment tree ver equals 1.
void get(int v, int lpos, int rpos, int ver)
{
if (SegTree[v][ver].sum == 0) return;
if (lpos == rpos)
{
s[lpos] = ver + 'a';
return;
}
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos, ver);
get(2 * v, lpos, mid, ver);
get(2 * v + 1, mid + 1, rpos, ver);
}
The main part of the program. Read the input data. Based on the input
string s, build 26 segment trees – one for each letter of the Latin
alphabet.
cin >> n >> q;
cin >> s;
s = " " + s;
build(1,1,n);
Process q queries sequentially.
for (i = 0; i <
q; i++)
{
cin >> l >> r >> command;
Perform a counting sort of all letters in the range [l; r]. To do this, first
count the number of occurrences of each letter ‘a’ + j in this interval
and store the result in cnt[j].
for (j = 0; j <
ALPHABET; j++)
cnt[j] = Summa(1, 1, n, l, r, j);
Then, starting from position pos, we’ll move to the right or to the
left depending on the value of the variable command.
pos = (command == 1) ? l : r;
for (j = 0; j <
ALPHABET; j++)
{
if (!cnt[j]) continue;
SetValue(1, 1, n, l, r, 0, j);
if (command)
{
SetValue(1, 1, n, pos, pos + cnt[j] - 1,
1, j);
pos += cnt[j];
}
else
{
SetValue(1, 1, n, pos - cnt[j] + 1, pos,
1, j);
pos -= cnt[j];
}
}
}
The generation of the resulting string is performed based on the contents
of the segment trees. The function get(1, 1, n, i), using the data from the i‑th
segment tree, places all letters ‘a’
+ i at their corresponding
positions in the string s. The get function performs a complete
push, traversing all vertices of the segment tree in O(n) time.
for (i = 0; i <
ALPHABET; i++)
get(1, 1, n, i);
Print the resulting string.
cout << s.substr(1);